
MATEMATİK
EĞLENCELİDİR
8. Yüz yılda, İran, Orta Doğu, Orta Asya, Kuzey Afrika, İberya ve Hindistan’ın bir Bölümü boyunca kurulan İslam imparatorluğu (Hilafet) matematiğe önemli katkılarda bulunmuştur. Her ne kadar matematik konusunda yazılmış olan İslam'i metinlerin çoğu Arapça yazılmışsa da, bir çoğu, Helenistik dünyada Yunancanın durumuna benzediğinden, Arapça, İslam dünyasının başından sonuna dek, o zaman, Arap olmayan Bilginlerin yazılı dili olarak kullanıldığından Araplar tarafından yazılmamıştır.
9. Yüz yılda İranlı matematikçi Muhammed ibn Mūsā al-Khwārizmı, için Hint – Arap sayı sistemi ve denklemlerin çözülmesi için yöntemler hakkında çeşitli önemli kitaplar yazdı. Al-Kind nin çalışması ile birlikte, onun, yaklaşık 825 yılında yazdığı Hint sayı sistemleri ile hesaplama hakkındaki kitabı, Hint matematiğinin ve Hint sayı sisteminin Batıya yayılması konusunda etkili olmuştur. Algoritma kelimesi, Algoritma’nın adının Latince'ye çevrilmesinden türetilmiştir ve Cebir kelimesi ise, onun çalışmalarından birinin başlığından alınmıştır , Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala (Sonuçlandırma ve Dengeye almanın Hesaplaması hakkındaki Özet kitap) . O, artı köklü ikinci dereceden denklemlerin cebirsel çözümü konusunda geniş kapsamlı ve ayrıntılı bir açıklama yapmış olup, temel biçimde ve kendi iyiliği için cebiri öğreten ilk kişi idi. O, aynı zamanda, denklemin artı taraflarında benzer terimlerin iptali olan çıkartma işlemi uygulanmış terimlerin denklemin diğer tarafına aktarılmasına istinaden uygulanan temel “indirgeme” ve “dengeleme” yöntemini tartıştı. Bu, al-jabr olarak başlangıçta tarif edilen operasyondur. Onun cebiri, artık çözülmesi gereken bir dizi problem ile ilgili değildi, ancak, açıklama, bundan böyle açıkça çalışmanın doğru nesnesini oluşturan denklemler için olası tüm prototipleri vermesi gereken içinde kombinasyonlar bulunan ilkel terimler ile başlayan bir açıklamadır”. O, aynı zamanda kendi menfaati açısından bir denklem üzerinde çalıştı ve bir soysal tarzda, basit şekilde problemin çözümü esnasında ortaya çıkmayacak şekilde olduğu kadar, ancak sonsuz sınıftaki problemlerin tanımlanması için özellikle başvuruldu.”.
Al-Karaji tarafından cebirdeki diğer gelişmeler oldu onun İlmi eserinde bilinmeyen miktarların tam sayının kuvvetlerini ve tem sayının köklerini birleştirmek için yöntem bilimini genişlettiği durumda al-Fakhri bu işlemleri uyguladı. Bazen matematiksel tümevarım ile ispat edilmeye yakın durum, MS 1000 yılında Al-Karaji tarafından yazılan bir kitapta ortaya çıkar ve o, binomial teoremi ve Paskal’ın üçgenini ve integral küplerini ispat için onu kullandı. Matematik tarihçisi F. Woepcke, Al-Karaji yi “cebirsel hesapların teoerisini ilk açıklayan kişi olarak” övdü. Ayrıca, 10. yüz yılda Abul Wafa, Diophantus’un çalışmalarını Arapça ‘ya çevirdi. Ibn al-Haytham, herhangi entegral kuvvetlerinin toplamı için genel formülü tespit etmek amacıyla, dördüncü kuvvetlerin toplamı için formül türeten ilk matematikçi idi.
O, bir paraboloitin hacmini bulmak amacıyla bir integrasyon işlemi yaptı ve dördüncü dereceye kadar polinomların entegrali için bulduğu sonucu genelleştirebilecek idi. O, böylece, polinomların entegrali için bir genel formül bulmaya çok yaklaştı ancak o, dördüncü kuvvetin üstündeki herhangi polinomlarla ilgili değildi.
11 yüz yılın sonlarında, Ömer Hayyam, Öklitte yaşanan güçlüklerle ilgili tartışmaları ele alan bir kitap yazdı. Bu kitap, Öklidin elemanları içindeki kusurları algılayan bu kitap özellikle paralel postülat üzerinde yoğunlaşmış idi. O, ayrıca kübik denklemlerin genel geometrik çözümünü bulan ilk kişi idi.[ alıntı gerekli]. O, aynı zamanda takvim reformu konusunda çok etkili idi. 13. yüz yılda, Nasir al-Din Tusi (Nasireddin), küresel geometri konusunda ilerlemeler gösterdi. O, aynı zamanda Öklit’in paralel postülatı konusunda etkili çalışmaları yazdı.
15. yüz yılda, Ghiyath al-Kashi, π nin değerini 16. ondalık basamağa kadar hesapladı.
Kashi aynı zamanda, daha sonra Ruffini ve Horner tarafından birçok yüzyıl sonra verilen yöntemlerin özel bir durumu olan n’nin köklerini hesaplamak için bir algoritmaya sahip idi.
Bu dönem içinde Müslüman matematikçilerin diğer edinimleri ondalık nokta notasyonundan Arap sayı sistemlerine ilaveyi içermektedir, sinüs dahil, tüm modern trigonometrik fonksiyonların keşfedilmesi için Al-Kindi'nin şifre analizi ve frekans analizinin takdimi, analitik geometrinin Ibn al-Haytham tarafından geliştirilmesi, Ömer hayam tarafından cebirsel geometrinin başlangıcı ve al-Qalasādī tarafından cebirsel notasyonun geliştirilmesi de diğer edinimler olarak sayılabilir.
15. yüzyıldan itibaren, Osmanlı İmparatorluğu ve Safevi Hanedanı dönemi esnasında İslam'i matematiğin gelişmesi durgunluğa girdi. Ortaçağ Avrupası matematiği
Matematik ile ilgilenen Ortaçağ Avrupası, modern matematikçilerin ilgisinden oldukça farklı olarak ele alındı. Bu konuyu işleten öğelerden biri, matematiğin doğanın yaratılmasının anlaşılması için anahtar sağladığı inancı, sıkça Plato’nun Timeos de gerekçelendirildi ve “Tanrı, ölçüm, sayı ve ağırlık olarak her şeyi emretti” şeklinde incile ait (Akıl kitabındaki) pasaj oldu.
Boethius, aritmetiğin, geometrinin, astronomi ve müziğin tarif edilmesi amacıyla quadrivium terimi için bir ad bulduğunda, 6. yüz yılda matematik için müfredat programında bir yer sağladı. O, Öklidin Elemanlarından alınmış bir dizi alıntı olan Nicomachus’un Yunanca ‘dan serbest (ücretsiz) çeviride Aritmetiğe Girişinde, De institutione arithmetica’ı yazdı; De institutione musica, da ayrıca Yunan kaynaklarından türetilmiştir. Onun çalışmaları pratik değil, teorik idi ve Yunan ve Arapça matematik çalışmalarının keşfine dek bu çalışmalar matematik çalışmanın dayanakları idi.
12. Yüz yılda, Avrupa’lı bilim adamları, özellikle al-Khwārizmī'nın tarafından yazılmış ve Robert of Chester, tarafından Latince’ye çevrilmiş olan Sonuçlandırma ve Dengeye almanın Hesaplaması hakkındaki Özet kitabı ve Adelard of Bath, Herman of Carinthia, and Gerard of Cremona. Tarafından çeşitli sürümleri çevrilmiş metinler dahil, bir bilimsel Arapça metin aramak amacıyla İspanya ye gittiler.
Ayrıcai, bkz: 12. Yüzyılın çevirileri
Bu yeni kaynaklar, matematiğin yenilenmesini harekete geçirdiler. Fibonacci, 1202 yılında özgür abaküs de yazı yazarak ve bu yazıyı 1254 de güncelleştirerek, Avrupa da Eratosthenes zamanından beri bin yıldan fazla bir boşluktan sonra ilk dikkate değer matematiği üretti. Hint – Arap sayı sistemleri çalışması Avrupa ya sunuldu ve diğer birçok matematik problemi tartıştı.
14. yüz yıl, geniş kapsamlı problemlerin araştırılması için yeni matematiksel kavramların geliştirilmesini gördü. Önemli bir katkı, yerel hareketin matematiğinin geliştirilmesi idi.
Thomas Bradwardine, , F Kuvvetinin R direncine oranı geometrik orantıda artarken V hızının aritmetik orantıda artacağını önerdi. Bradwardine, bunu bir dizi özel örnek ile açıkladı, ancak logaritma henüz tasarlanmış olmayacağından, : V = log (F/R) yazarak sonucu içinde bulunulan döneme uygun düşmeyen bir biçimde ifade edebileceğiz.
Bradwardine'nin analizi, ilaçların terkiplerinin doğasının farklı fiziksel bir probleme sayılaştırılması amacıyla, al-Kindi ve Arnald of Villanova tarafından kullanılan matematiksel tekniğin aktarılması konusunda bir örnektir.
14 Yüz yıl Oxford hesaplamacılardan biri olan William Heytesbury, diferansiyel hesabı ve sınırların kavramı olmaksızın, anlık hızın ölçülmesini önerdi. "tarif edilmesi gereken yöntem ile [bir gövde ] ile eğer... o daima, içinde verilen anda hareket ederek, aynı tarzda, aynı hız derecede hareket etmiş ise”
Heytesbury ve diğerleri “düzgün olarak hızlanan bir harekete maruz bir gövde (bu gün integrasyon ile çözümlendi) ile kaplı mesafeyi, bir hareketli gövdenin daima aynı tarzda [hız] (hızın) artımını elde etmesi ya da kaybetmesi şeklinde, orta derece bir hızla devamlı hareket halinde ise, verilen bir süre içinde enine geçeceğini matematiksel olarak tespit etti.
Paris üniversitesinde, Nicole Oresme ve Italyan Giovanni di Casali,hattın altındaki alanın sabit ivmeyi gösterdiğini ve seyredilen toplam mesafeyi temsil ettiğini iddia ederek, bağımsız şekilde bu ilişki konusunda grafik gösterimler sağladılar. Öklidin elemanlarının daha sonraki matematiksel açıklamasında Oresmo, bir gövdenin tek sayıları arttıracak şekilde, herhangi bir niteliğin elde edileceğini göstererek her bir ardışık süre artımında daha ayrıntılı bir analiz yaptı. Öklit tek sayıların toplamının tam kare sayılar olduğunu, gövde tarafından elde edilen toplam niteliğin, sürenin karesi olarak artacağını göstermiştir.
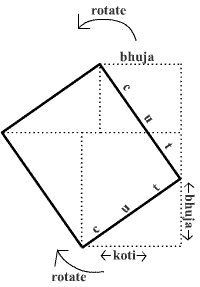
Yuktibhāṣā (Cebirin ilk metin kitabı) içinde sinüs kuralının açıklanması